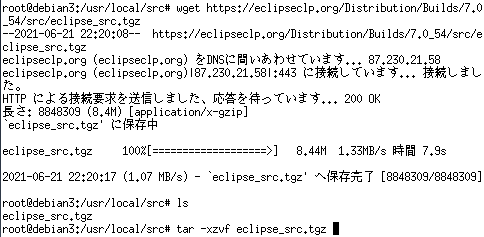
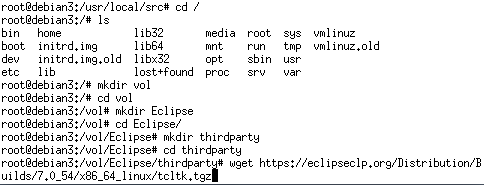
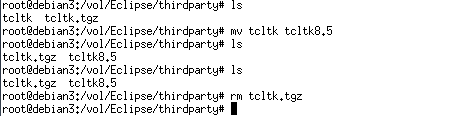
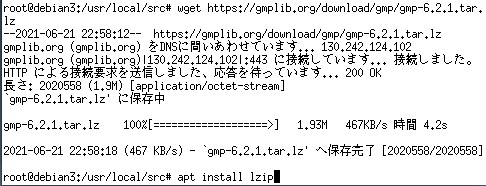
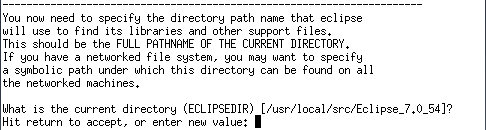
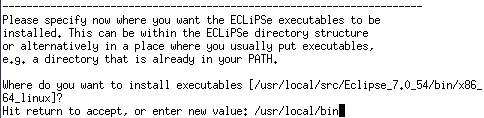
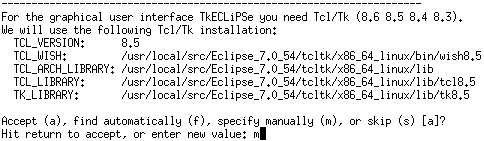
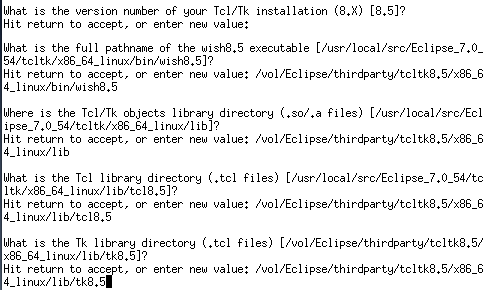
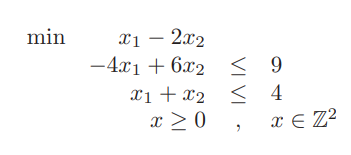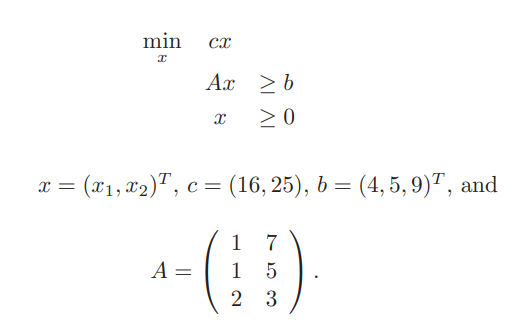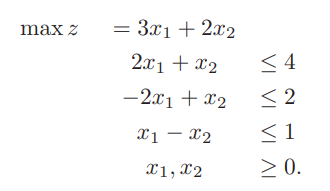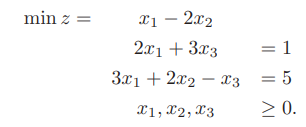ECLiPSe CLPでグラフの最小カットを求める方法を説明します。
グラフのカットというのは、最大流問題で用いた、エッジに許容流量の設定のあるスタートとゴールのノードを持つ有向グラフのすべてのノードを、「スタート側」「ゴール側」の2種類のノードに分けることをいいます。
ノードをどのように分けてもよいので、カットの仕方には複数通りの方法があります。
グラフに|V|個のノードがあったとして、スタートとゴールのノードのみどちら側か決まっているので 2^(|V|-2)通り のカットの方法があります。
最小カットというのは、複数あるカットのうち、「カット容量が最小となるもの(そしてその容量)」のことを言います。
カット容量とは、ノードとノードを結ぶすべてのエッジのうち「スタート側に属するノード」から「ゴール側に属するノード」の方向のエッジの許容流量の総計のことを言います(スタート側→スタート側、ゴール側→ゴール側、ゴール側→スタート側 のエッジの容量は数えない)
最小カット容量は、スタート→ゴールの流れのボトルネックのようなもので、この値がそのまま最大流と等しくなるとのことです。
(最小カット容量=最大フロー)
前置き長くなりましたが上記最小カットを求めます。
library(all_min_cuts) の述語 all_min_cuts/8 を使います。
all_min_cuts(+Graph, +CapacityArg, +SourceNode, +SinkNode, -MaxFlowValue, -MaxFlowEdges, -MinCuts, -MinCutEdges)
Grapha – グラフ
CapacityArg – エッジ e(_,_,A) のAのどこが最大流量か設定する
SourceNode – スタートのノード番号
SinkNode – ゴールのノード番号
MaxFlowValue – 最大フロー(=最小カット容量)(戻り値)
MaxFlowEdges – 「フロー - エッジ」のリスト(戻り値)
MinCuts – 最小カット容量をもつカットのリスト(複数あれば複数)(戻り値)
MinCutEdges – すべての最小カット組(それぞれのカット組はスタート側-ゴール側を分けるエッジのリスト)(戻り値)
①以下の図でノード1がスタート、ノード7がゴールとして最小カットを求めます。
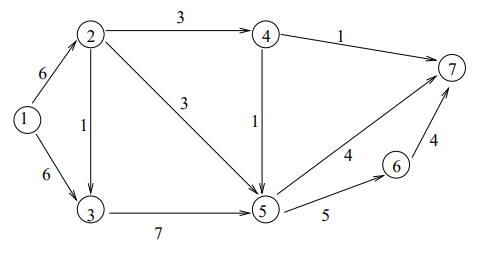
プログラム:
:-lib(graph_algorithms).
:-lib(all_min_cuts).
solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges):-
make_graph(
7,
[
e(1,2,6),
e(1,3,6),
e(2,3,1),
e(2,4,3),
e(2,5,3),
e(3,5,7),
e(4,5,1),
e(4,7,1),
e(5,7,4),
e(5,6,5),
e(6,7,4)
],
Graph),
all_min_cuts(Graph, 0, 1, 7, MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).
実行結果(見やすいように手で改行入れてます):
?- solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).
MaxFlowValue = 9
MaxFlowEdges =
[
4 - e(6, 7, 4),
4 - e(5, 7, 4),
4 - e(5, 6, 5),
1 - e(4, 7, 1),
1 - e(4, 5, 1),
4 - e(3, 5, 7),
3 - e(2, 5, 3),
2 - e(2, 4, 3),
4 - e(1, 3, 6),
5 - e(1, 2, 6)
]
MinCuts = [[2, 5, 3, 6, 1, 4]]
MinCutEdges =
[
[
e(4, 7, 1),
e(6, 7, 4),
e(5, 7, 4)
]
]
Yes (0.00s cpu)
最小カットは9で
ノード 4-7、6-7、5-7 のエッジがスタート側とゴール側を分けるエッジのようです。
②以下のグラフで最小カットを求めます。
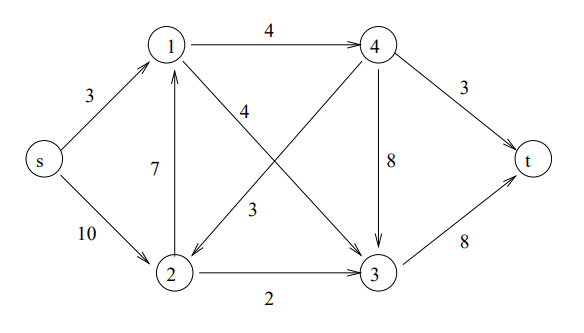
プログラム(便宜的にスタートノードとゴールノードをそれぞれノード5、ノード6に置き換え):
:-lib(graph_algorithms).
:-lib(all_min_cuts).
solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges):-
make_graph(
6,
[
e(5,1,3),
e(5,2,10),
e(1,4,4),
e(1,3,4),
e(2,1,7),
e(2,3,2),
e(4,2,3),
e(4,3,8),
e(4,6,3),
e(3,6,8)
],
Graph),
all_min_cuts(Graph, 0, 5, 6, MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).
実行結果:
?- solve(MaxFlowValue, MaxFlowEdges, MinCuts, MinCutEdges).
MaxFlowValue = 10
MaxFlowEdges =
[
7 - e(5, 2, 10),
3 - e(5, 1, 3),
3 - e(4, 6, 3),
1 - e(4, 3, 8),
7 - e(3, 6, 8),
2 - e(2, 3, 2),
5 - e(2, 1, 7),
4 - e(1, 4, 4),
4 - e(1, 3, 4)
]
MinCuts = [[2, 5, 1]]
MinCutEdges =
[
[e(1, 4, 4), e(1, 3, 4), e(2, 3, 2)]
]
Yes (0.02s cpu)
最大フロー(最小カット)10、
ノード1-4、1-3、2-3 を結ぶエッジがスタート側とゴール側を結ぶ