CLPFDライブラリ読み込んでるけど使ってなかった…
:-use_module(library(clpfd)). adding(1,0):-!. adding(Idx,Sum):- (Idx mod 3 =:= 0 ; Idx mod 5 =:= 0), !, Idx1 is Idx - 1, adding(Idx1,Sum1), Sum is Sum1 + Idx. adding(Idx,Sum):- !, Idx1 is Idx - 1, adding(Idx1,Sum).
実行結果
[1] 2 ?- adding(999,R).
***********************(解答伏せます)**********************
2週間ほど前にProject Eulerの存在を知り、面白いのでチャレンジしている。本日の時点では26問解いた。全部Prologで解いている。
ところどころCLPFDを使える問題があり、使っている。
制約論理プログラミングの動作の特徴？みたいなのを感じられる面白い問題があったので、紹介しようと思う。
この問題は、CLPFDだと探索の処理を一切書かずに以下のようにただ定義だけをずらずら書くだけで解ける。
:-use_module(library(clpfd)). solve(Sum):- [A,B,C] ins 1..1000, A+B+C#=Sum, A*A + B*B #= C*C, A #< B, B #< C, label([A,B,C]), write([A,B,C]).
問題の条件をそのまま書いただけのようなプログラムだけど、本当にこれだけで解けます。
ただ、これだと非常に処理時間がかかかる。僕のしょぼいマシンでは、
以下のように150秒かかった。
1 ?- time(solve(1000)). 回答伏せます % 69,897,996 inferences, 142.641 CPU in 153.188 seconds (93% CPU, 490029 Lips) true
ネットで調べるとこのピタゴラス数の法則のようなものがいくつかヒットするのですが、そのひとつが以下の図のようなもので、
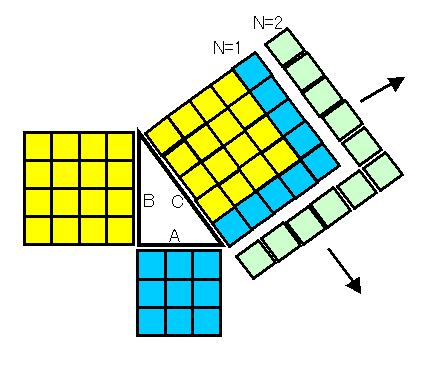
ようするにBとCの関係に関してなのですが、長さBの正方形の辺を1つづつ大きくして一回りづつ囲むように配置してゆくといつか長さCの正方形と等しくなるというもので、しかもこの大きくした分の面積はA × Aと等しいというもの。
大きくした分の面積は、N(=1,2,3..)の数列として以下のように表すことができる。
En = 2 × N × B + N × N
そして、A × A = En
前述のプログラムにこの条件を追加して動作させると、答えを出す速度が段違いに速くなる。
:-use_module(library(clpfd)). solve(Sum):- [A,B,C] ins 1..1000, A+B+C #= Sum, A #< B, B #< C, A * A + B * B #= C * C, A*A #= 2*N*B+N*N, % 追加した条件 N in 1..1000, % 追加した条件 label([A,B,C]), write([A,B,C]).
実行結果：
[4] 6 ?- time(solve(1000)). 回答伏せます % 14,116,046 inferences, 16.094 CPU in 16.516 seconds (97% CPU, 877114 Lips) true
10倍近く速くなった。
多分Aの探索空間が新しい条件の数列で絞り込まれて速くなるのだと思う。
「思う」と書いたのも制約論理プログラミングの特徴といえば特徴で、条件を書くたびに大量の制約伝播用のプログラムが内部で自動的に生成されるため、厳密な動作が非常に追いずらい。ステップ実行などのデバックもしずらい(CLPFDライブラリ内部で自動的に大量のバックトラックが発生している）。
これは悪い面で、動作が見積もれないことが原因となり正確・確実な動作を期待される産業分野でなかなか採用されないかもしれない。ちゃんとした企業ほど異常動作のときなどの原因追及フェーズを徹底的に行っているので、そのときに｢思う」とか｢これ入れたら速くなるかも」とかは通用しないわけです。動作確認のためのログを埋め込むのも結構大変です（ライブラリに直接埋め込まないと駄目だし制約伝播状態を出力した解析困難なログになることが予想される）
ちなみに制約伝播というのは、prolog の attributed_variableの仕組みを使って変数の探索空間が変更された時点でキックされる述語が予約されていて、ドミノ倒しのように次々と他の変数の探索空間をせばめてゆくという手法です。
CLPFDのソースを読んでゆくとわかるのですが A in 1..500 などという探索空間は木構造で表現されており、探索空間の変更はこの木構造を変えることで行っている。
たとえば A の木構造が最初 左の枝が1、右の枝が500 の状態で、この状態から100～200の可能性がないことが判明した時点で、右の500の枝の部分に100..200のノードが新しく追加される感じ？
Prologの変数は基本的に再代入不可なのですが、attributed_variableは再代入可能かつ履歴情報を保持していてバックトラック時に直前の値に戻る（Prologの通常の自由変数はバックトラック時は未設定状態になるだけで履歴情報は持っていない）ようなのでこれを利用しているのでしょう。
CLPFDは非常に簡単に記述できて問題が解けるため、勉強し始めのころはまるで魔法のツールのようだと感じたが、上記のような、問題自身の性格を表す条件を入れないとすぐに処理時間が膨大になってしまうように感じる。
当たり前のことだが、問題に対する洞察・分析も非常に大切ということだろう。